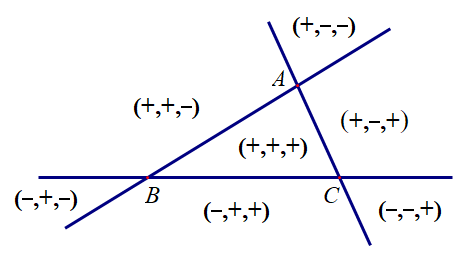1. 奔驰定理
在讲平面向量的时候,遇到了一个经典的题目:
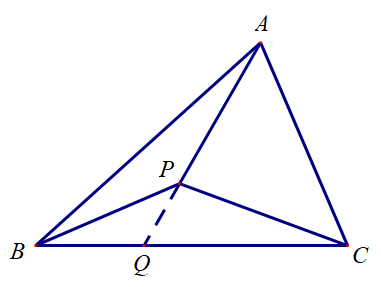
已知点 P 为 △ABC 内一点,求证:S△PBC⋅PA+S△PCA⋅PB+S△PAB⋅PC=0.
证明如下:如图,延长 AP 交 BC 于 点 Q,则 S△PCA+S△PABS△PBC=∣AP∣∣PQ∣,
故 PQ=−S△PCA+S△PABS△PBC⋅PA.
另外,因为 ∣BQ∣:∣QC∣=S△PAB:S△PCA,所以 PQ=S△PCA+S△PABS△PCA⋅PB+S△PAB⋅PC,
故 −S△PBC⋅PA=S△PCA⋅PB+S△PAB⋅PC,移项后命题得证.
![]()
这个结论因为它的图形长得像奔驰的标志,被称为“奔驰定理”.
这个名字最早的出处不详,但实际上,这对应的就是三角形的“重心坐标”.
2. 三角形的重心坐标
对 △ABC 所在平面内任意一点 P,如果存在不全为零的实数 λ0,λ1,λ2,使得
(λ0+λ1+λ2)OP=λ0OA+λ1OB+λ2OC
对平面内任意一点 O 成立,则称 (λ0:λ1:λ2) 为点 P 相对于 △ABC 的重心坐标.
显然,重心坐标并不是唯一的,(kλ0:kλ1:kλ2) 也是点 P 相对于 △ABC 的重心坐标.
为了保证唯一性,我们可以进行对其正规化,取 λi′=λi/k=0∑2λk ,则 i=0∑2λi′=1,此时称 (λ0′:λ1′:λ2′) 为其正规化(重心)坐标.
2.1. 重心坐标的存在性
对 △ABC 所在平面内任意一点 P,根据平面向量基本定理,存在唯一的实数对 (λ,μ),使得 AP=λAB+μAC.因此
OP=OA+AP=OA+λAB+μAC=OA+λ(OB−OA)+λ(OC−OA)=(1−λ−μ)OA+λOB+μOC
取 (λ0,λ1,λ2)=(1−λ−μ,λ,μ) 即可.注意这已经是正规化坐标.
2.2. 正规化坐标的符号
当点 P 位于 △ABC 内部的时候,λ,μ,λ+μ∈(0,1),故 1−λ−μ∈(0,1),也就是三项均是正数.
对于 △ABC 外的情况,可以参考下图:
![]()
2.3. 重心坐标的几何意义
在平面直角坐标系 xOy 中,设 A(x1,y1),B(x2,y2),C(x3,y3),P(xP,yP),点 P 相对于 △ABC 的重心坐标为 (α:β:γ),其中 α+β+γ=1.
根据定义,OP=αOA+βOB+γOC,
因此
⎩⎨⎧xPyp1=αx1+βx2+γx3=αy1+βy2+γy3=α+β+γ⟺xPyP1=x1y11x2y21x3y31αβγ
根据 Cramer 法则,
α=S△ABCS△PBC,β=S△ABCS△PCA,γ=S△ABCS△PAB
这里的面积指的是三角形的有向面积,正负与三个点的位置关系有关.
所以,(S△PBC:S△PCA:S△PAB) 就是点 P 相对于 △ABC 的重心坐标,这对应的就是“奔驰定理”中的三个系数.
实际上,根据“奔驰定理”,
S△PBC⋅(OA−OP)+S△PCA⋅(OB−OP)+S△PAB⋅(OC−OP)=0
移项得
(S△PBC+S△PCA+S△PAB)⋅OP=S△PBC⋅OA+S△PCA⋅OB+S△PAB⋅OC
也可以直接得到,当点 P 在 △ABC 内部的时候,它相对于 △ABC 的重心坐标为 (S△PBC:S△PCA:S△PAB).
由于三角形的重心坐标和面积有关系,因此也被称为面积坐标.
2.4. 重心坐标名称的来源
考虑平面内三个质点 A、B、C,它们的质量分别为 m1、m2、m3,则该质心系的质心相对于 △ABC 的重心坐标恰好为 (m1,m2,m3).
3. 三角形各中心的重心坐标
下表列出了几个常见的三角形中心的重心坐标.
| 名称 |
重心坐标 |
| 重心 |
1:1:1 |
| 内心 |
a:b:c |
| 外心 |
a(b2+c2−a2):b(c2+a2−b2):c(a2+b2−c2)
sin2A:sin2B:sin2C
(1−cosBcosC):(1−cosCcosA):(1−cosAcosB) |
| 垂心 |
(a2+b2−c2)(a2−b2+c2):(−a2+b2+c2)(a2+b2−c2):(a2−b2+c2)(−a2+b2+c2)
tanA:tanB:tanC
acosBcosC:bcosCcosA:ccosAcosB |
| 旁心 |
−a:b:ca:−b:ca:b:−c |
其它特殊点的重心坐标,可以查看 ETC,里面每个点下面列出的 Barycentrics 就是该点的重心坐标.
4. 重心坐标的一般定义
事实上,重心坐标的定义可以推广到 n 维向量空间,甚至是仿射空间.
考虑 n 维仿射空间 A 中的仿射无关的 n+1 个点 A0,A1,⋯,An,即 A0,A1,⋯,An 是一个 n 维单形的顶点,则对于任意一点 P∈A,存在不全为零的实数 λ0,λ1,⋯,λn,使得
(λ0+λ1+⋯+λn)OP=λ0OA1+λ1OA2+⋯+λnOAn
对于任意一点 O 成立,则称 (λ0:λ1:⋯:λn) 为点 P 相对于 A0,A1,⋯,An 的重心坐标.
重心坐标是一种齐次坐标,在仿射变换下保持不变.
(λ0:λ1:⋯:λn) 和 (μ0:μ1:⋯:μn) 都是点 P 相对于 A0,A1,⋯,An 的重心坐标的充要条件是,存在非零常数 k,使得对于任意的 i,有 λi=kμi.
类似的,也可以对其进行正规化,取 i=0∑nλi=1 即可.