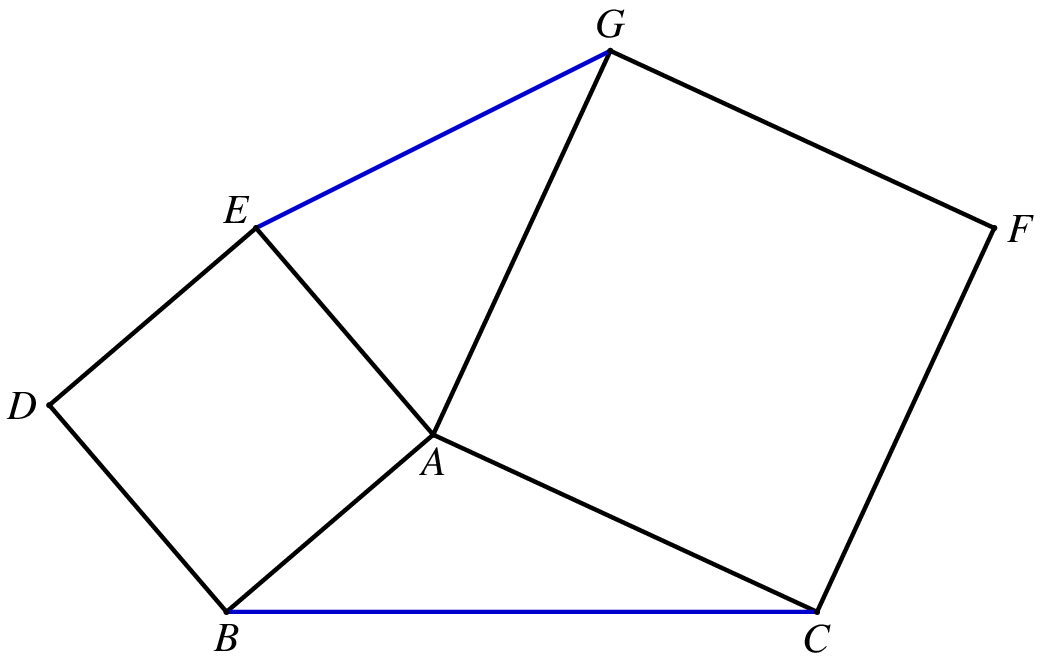
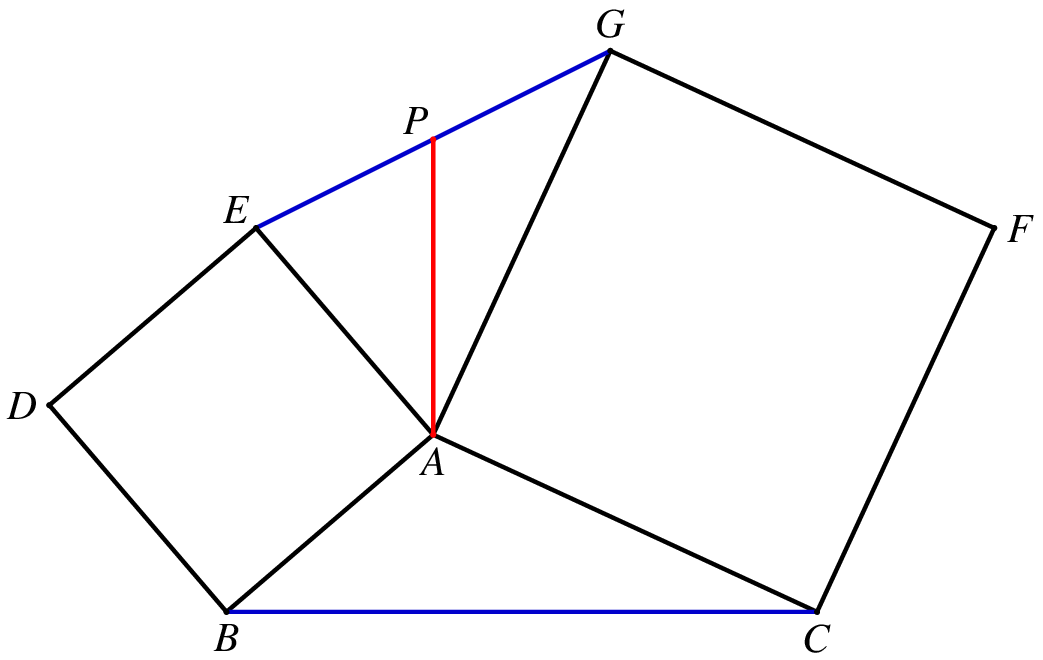
在正方形的题目中,有很常见的一类是和两个正方形有关的图形,如下图:
![图1]()
在这个图形中,有很多有意思的性质,也衍生出了很多的题目.我们讲分几次一一道来.
1. 「手拉手」模型
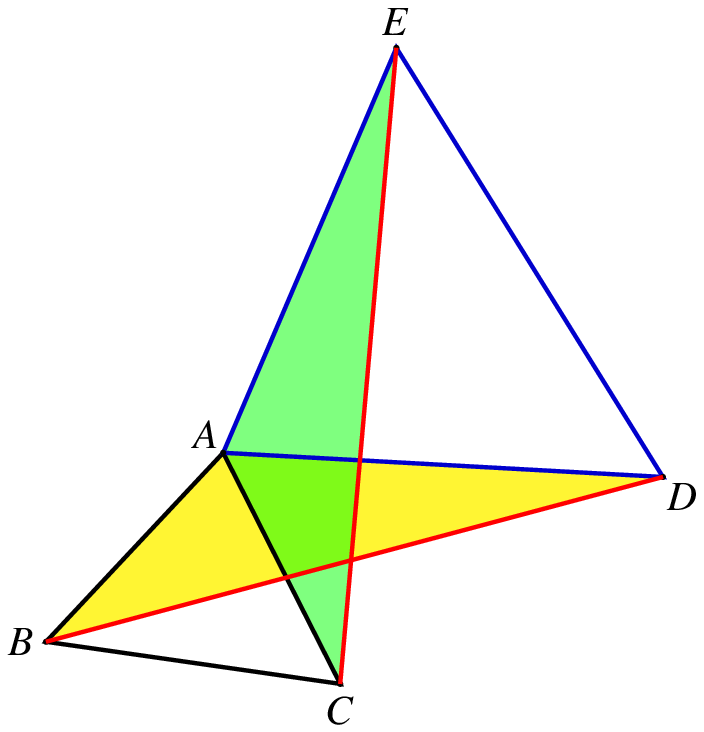
在学习全等的时候,我们知道有一类很重要的全等模型——旋转全等模型,俗称「手拉手」模型.说的是两个共顶点且顶角相等的等腰三角形,一定伴随着一组旋转全等,如图2:
![图2]()
△ABC 和 △ADE 是两个顶角相等的等腰三角形,易证 △ABD≅△ACE .这是一个旋转全等,旋转角度等于两个等腰三角形的顶角角度.
关于这个模型,也有很多相关的结论,不过大部分和这次的内容关系不大,有机会我们另开文讲述.
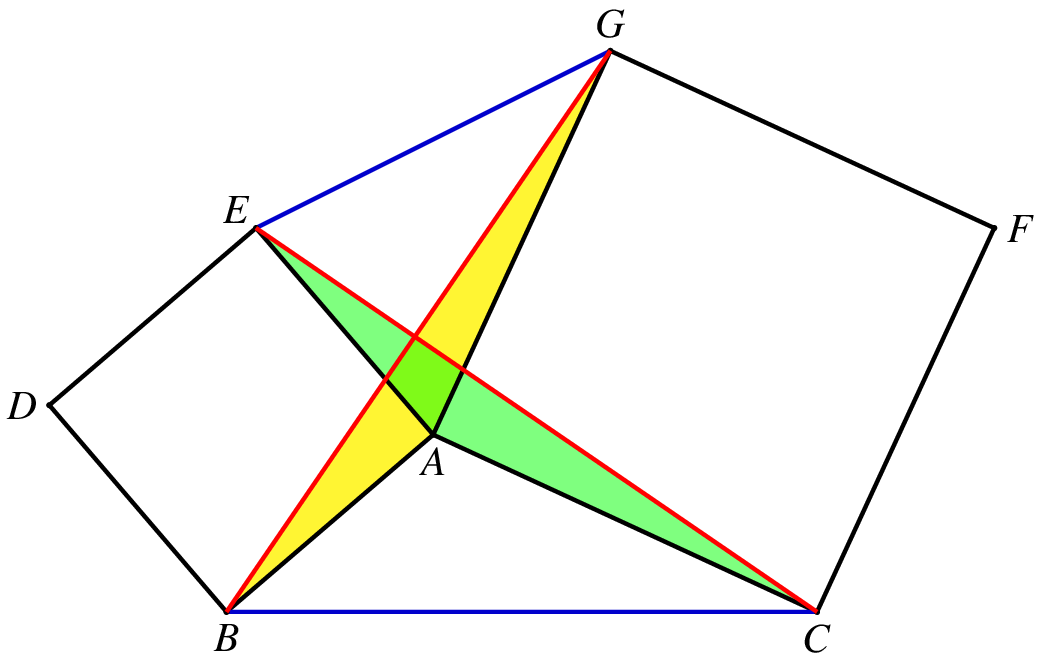
那么,对于两个共顶点的正方形,也有类似的结论.在图1中,我们可以把它看成是两个等腰直角三角形 ABE 和 ACG 的「手拉手」,于是就有 △ABG≅△AEC,而且旋转角度为 90∘.
![图3]()
于是,我们就得到了一个对角线垂直且相等的四边形 BCGE.
1.1. 和中点四边形相关的问题
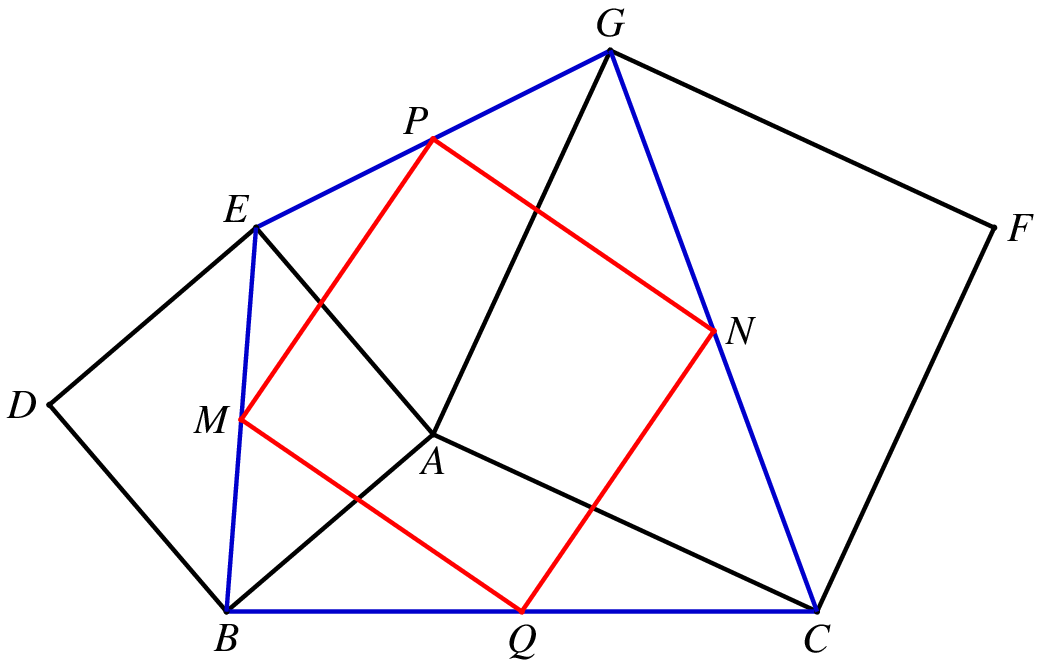
熟悉中点四边形的朋友马上就会想到,这样一个四边形的中点四边形一定是一个正方形,也就是下面这个图:
![图5]()
在这个图中,中点四边形 MPNQ 就是一个正方形.
2. 另一个和中点相关的问题
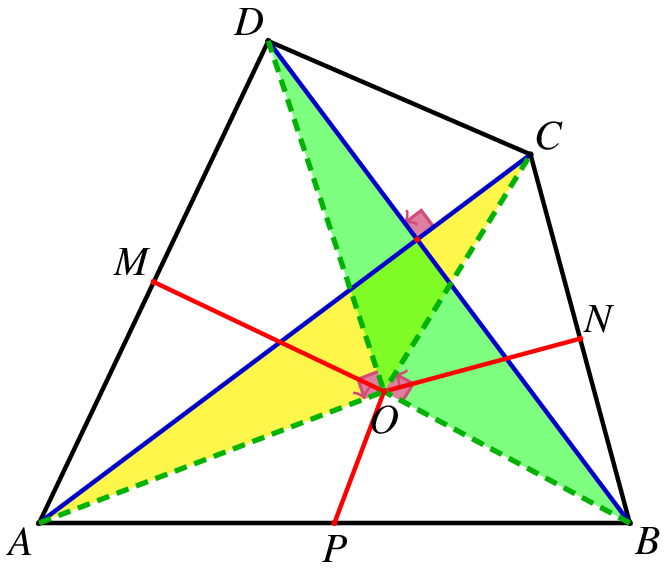
在图1中,如果我们取 EG 的中点 P ,连结 AP ,则 AP⊥BC 且 AP=21BC.(如果取 BC 中点,有类似的结论)
![图5]()
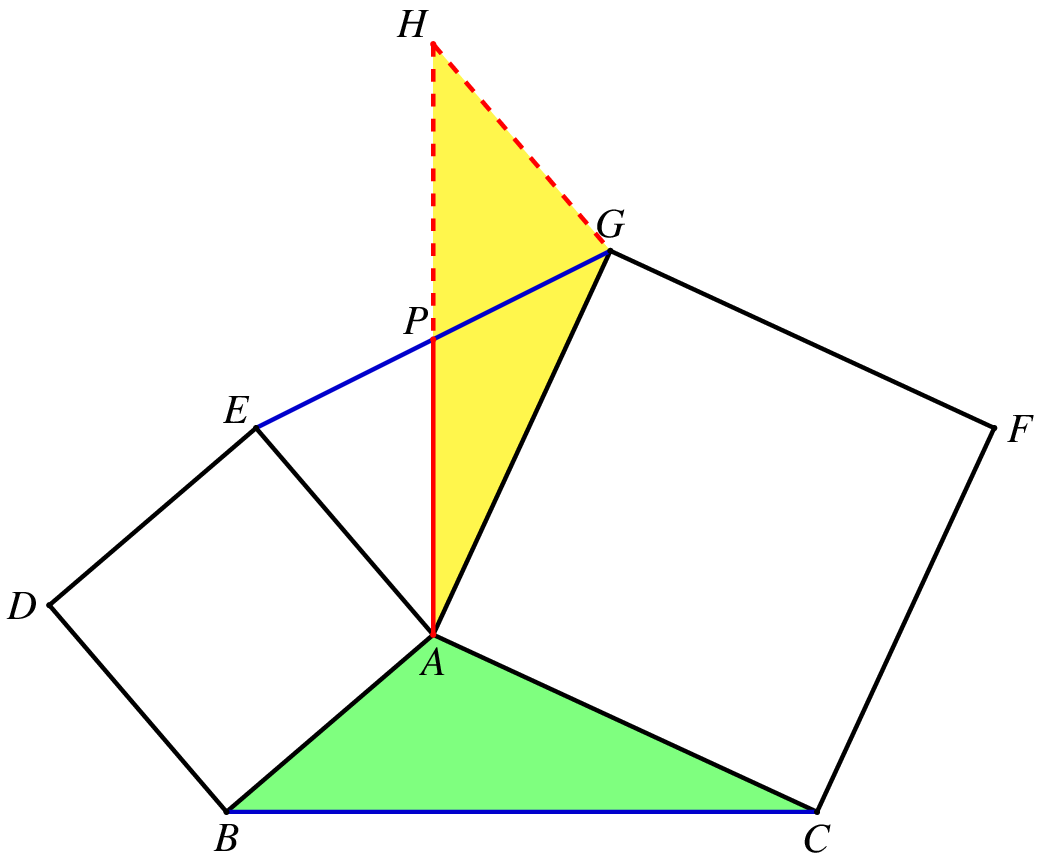
对于中点问题,我们知道一种常见的处理方法就是「倍长中线」,因此我们倍长 AP 至 H,可以证明 △GHA≅△ABC.注意这是一个旋转 90∘ 的全等,因此 AH 和 BC 垂直且相等,所以上面的结论成立.
![图6]()
这个命题逆命题也成立,即如果 AP⊥BC,则 P 为 EG 的中点,且 AP=21BC.
这个命题也可以利用上图来证明,不过这个时候需要直接延长作 AH=BC 来证明全等.
这个时候另外一种处理方法是做垂直,利用弦图的模型来证明全等.
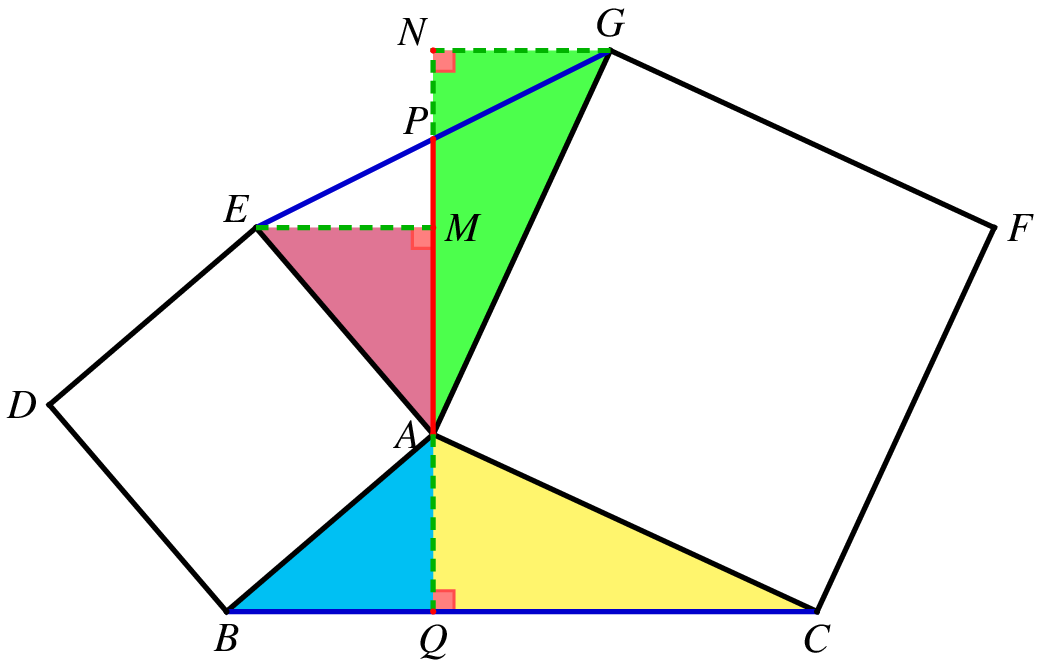
![图7]()
如图7,延长 PA 交 BC 于 Q,作 EM⊥AP 于 M,GN⊥AP 于 N,则 △ABQ≅△EAM,△ACQ≅△GAM,于是 EM=AQ=NG 且 EM∥NG,因此 EMGN 是平行四边形,于是
PEPNBC=PG,=PM,=BQ+QC=AM+AN=2AP
这两个证明同时还都证明了另一个结论,就是 S△ABC=S△AEG.由割补法知这两个三角形的面积的确是相等的.
当然,如果熟悉三角函数的话,这两个三角形的面积相等是显然的.因为 ∠BAC 和 ∠EAG 互补,而角的两边对应相等,因此面积也是相等的.
2.1. 变形一
前面我们说了 BCGE 是一个对角线垂直且相等的四边形,因此,这个题的可以这样来出:
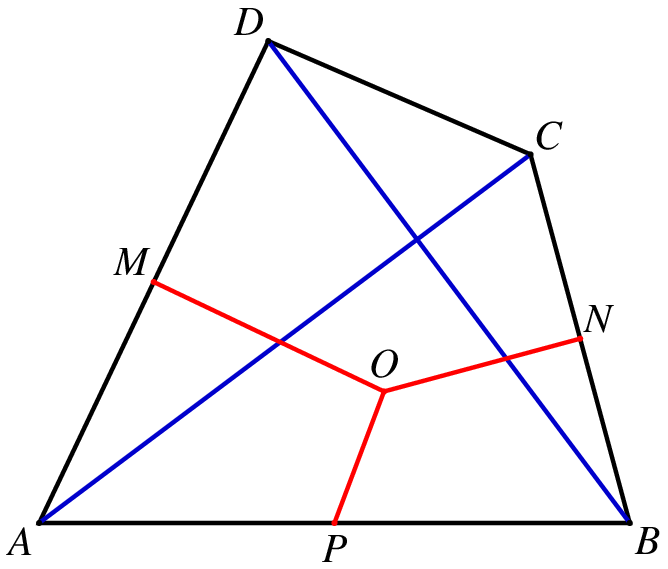
如图8,在四边形 ABCD 中,AC⊥BD,且 AC=BD,分别取 AD、BC、AB 的中点 M、N、P,分别过 M、N 作 AD、BC 的垂线交于 O,则 PO⊥CD.
![图8]()
这个图如果把 OA、OB、OC、OD 都连起来,显然有 △OAC≅△OBD,注意这是一个旋转 90∘ 的全等,因此 △OAD、△OBC 都是等腰直角三角形.于是这就变成了图5一样的图了,后面的证明和上面相同.
![图9]()
2.2. 变形二
如果我们把两个正方形中间再加一个小正方形,那么结论会变成什么样子?
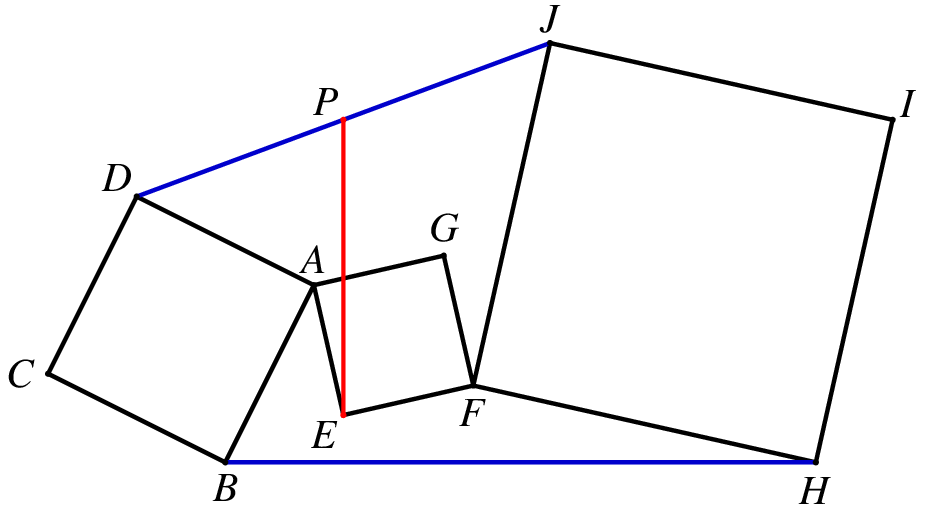
如图10,有三个正方形 ABCD、AEFG、FHIJ,取 JD 中点 P,则有 PE⊥BH 且 PE=21BH.
![图10]()
很明显,这个图是上面图5的一个推广,如果中间的小正方形缩成一个点,那么就变成了图5.
既然是推广,那么证明应该也是类似的.我们还是可以倍长 EP 来做,不过这个时候要找的全等变得复杂了一些.
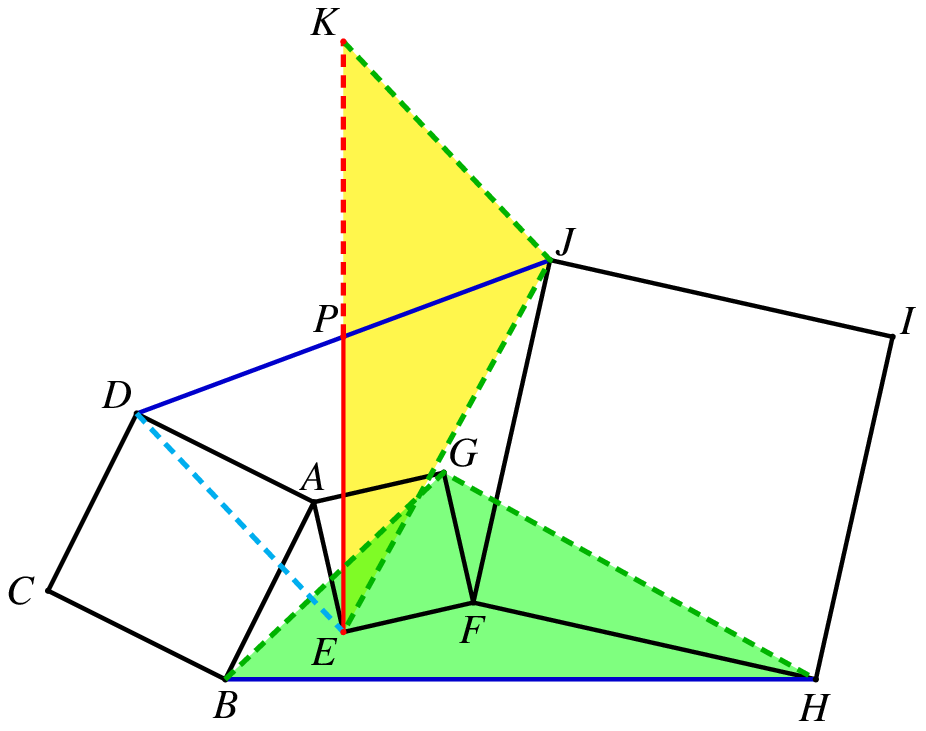
![图11]()
如图11,我们倍长 EP 至 K,可以类似地证明 △JKE≅△GBH.
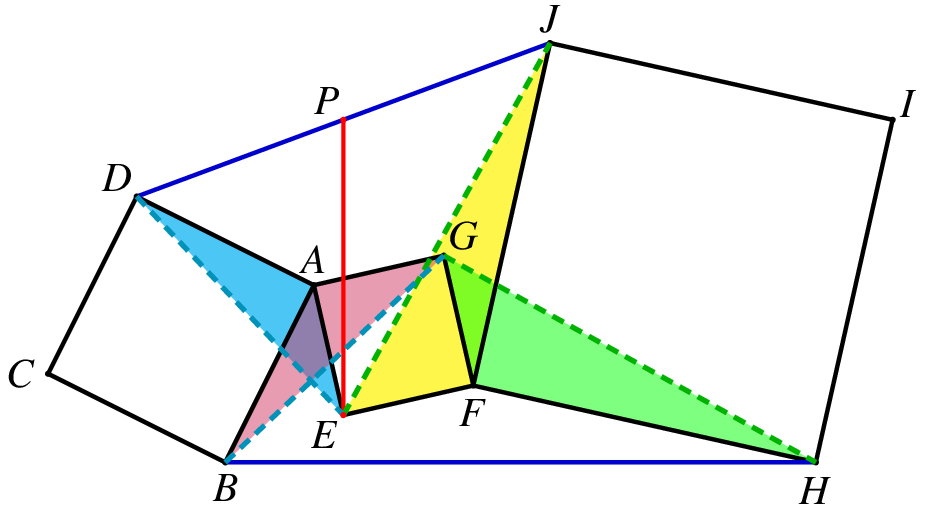
不过在证明的时候需要注意,这里面隐藏着两个「手拉手」的全等模型,在证明上面的全等的时候需要用到,如图12,有 △ADE≅△ABG,△FJE≅△FGH,都是旋转 90∘ 的全等.
![图12]()
2.3. 拓展联想
在圆的内接四边形中,有一个类似的结论:
若圆内接四边形的对角线相互垂直,则垂直于一边且过对角线交点的直线将平分对边.
这就是 Brahmagupta 定理,一般译作「婆罗摩笈多定理」,或者「布拉美古塔定理」.
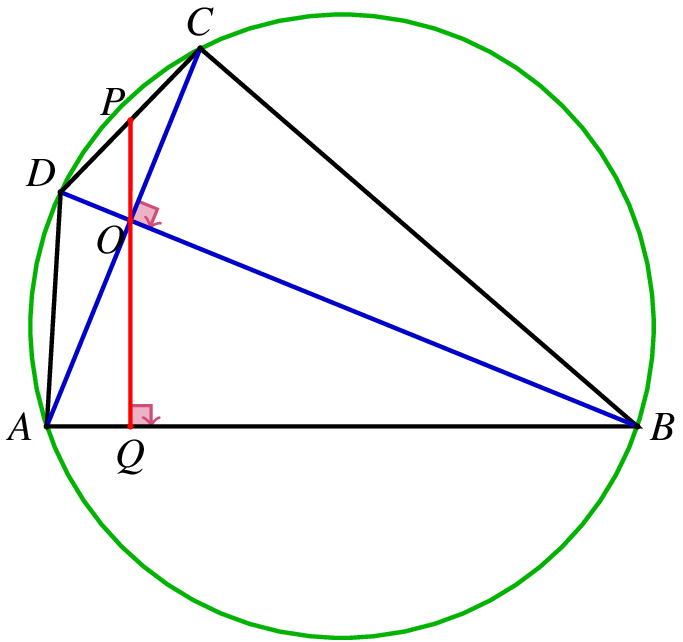
如图13,在圆的内接四边形 ABCD 中,AC⊥BD,过对角线的中点 O 作 PQ⊥AB 点 Q,交 CD 于点 P,则 P 是 CD 的中点.
![图13]()
这个的证明是比较简单的,
∠POC=90∘−∠QOB=∠QBO=∠PCO
于是
∠POD=90∘−∠POC=90∘−∠PCO=∠PDC
故 PC=PO=PD,直接倒角就可以证明了.
这个定理的逆命题也成立,即如果 P 是 CD 的中点,那么 OP⊥AB.证明和上面类似.
总结一下,这类问题主要是和中点有关系,主要的方法是「倍长中线」和「手拉手」的全等.还有一类问题是借助于中位线来解决的,这一类题目讨论的不是 EG 的中点(图1中),而是 DF 的中点.这一类问题,我们放到下一篇文章中来讨论.